Multiple Time Dimensions, why not?

One of the biggest misconceptions deep-rooted in the human mind is the one-dimensionality of time. When physicists discover a theory that calls for multiple extra dimensions, such as the string theory, their first reaction is to assign those extra as spatial dimensions. They do so because they abhor the plurality of time ^a).

In order to give the reason for their invisibility, the physicists hypothesize that the extra dimensions are curled up into tiny loops ^b). However, as there are so many possibilities on how those extra-dimensions may be curled up, the outcomes of such string theory can reach billions.  It gives us a good reason to allow the Occam razor getting rid of this dire hypothesis without delay.

Internal symmetry

The second reason for the invisibility of the extra-dimensions is that they are time dimensions. A world with multiple space and time dimensions certainly complies with the principle of the relativity. We would have in our worlds no more bizarre things such as donut-like or Calabi-Yau tiny manifolds. As such, the world may preserve its internal symmetry in which changing [reversibly] the time dimension with the space dimension leaves the physical laws identical. 

It is evident that the physical laws' formulation in the world with many time dimensions would be exceedingly complicated. However, we may have a more natural way to solve the formulation by transforming all but one time dimensions into space dimensions. Having done that,  we get a simple system of higher-dimensional space with only one temporal dimension without altering the outcome of the result. 

To give an illustration, let us take the example of our space (or 3-brane as you wish ^c)) which we interpret as embedded in a 10-ambient spacetime. Under multiple time dimensions framework, such a system consists of three space dimensions and seven temporal dimensions. By transforming all temporal dimensions  (except the highest dimensional one) into space dimensions, we get a system having nine space dimensions and one temporal dimension  (a 9-brane embedded in the same 10-ambient spacetime). The physical laws' formulation in the latter system is much simpler than that in the first one ^d).

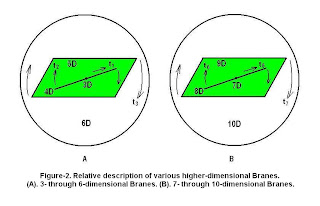
Under such a system we can also transform only some of the time dimensions into space dimensions and keep the remaining intact. As such, we would have various dimensional branes ranging from 3-brane to 9-brane embedding in the same 10-ambient spacetime without even changing the outcome of the result. 

These are the various dimensional branes which we encounter in the superstring theory. However, in most of the cases, each of those branes is assumed to have only one temporal dimension. As such, the physicists who deal with those branes have not any simple way to solve the respective formulation ^e). 

Even in dealing with the 9-brane, we may have no good solution. We may, in this case, extend the dimensions of the ambient spacetime higher and higher until we get the solution ^f). 

We may say that the higher the brane's dimensions are, the flatter it is.  This situation makes the mathematical formulation of the physical laws simpler.

Figure-1 diagrammatically shows how events which are not simultaneous at a particular time dimension t₁ become simultaneous at a higher time dimension t₂. It is as though space flatten out as the number of temporal dimensions becomes higher that makes the physical laws formulation more straightforward ^g).

Notes:

a)   Physicists wrongly regard the 4-spacetime as having three space dimensions and one temporal dimension which should be inherently multidimensional. The underlying of what we know as 4-spacetime is 4-dimensional time having a 3-dimensional cross-section (3-brane) in it.

b)   Kaluza and Klein first introduced Kaluzathe idea to unify the electromagnetic field with that of gravity by adding the curly fifth dimension to the classical four. Later on, the idea is extended for much higher dimensions in which the loop size of the extra dimensions is at the order of Planck size (10^-33 cm).

c)  We use the notations of space, hypersurface, hyper-interface or brane interchangeably.

d)   A system consisting of 3-space embedded in 10-dimensional ambient spacetime can be formulated as Hypercomplex function:

q = x₁ +x₂ + x₃ + ic₁t₁ + jc₂t₂ + kc₃t₃ +lc₄t₄ + mc₅t₅ + nc₆t₆ + oc₇t₇ 

under a coordinate patch consisting of three real x₁, x₂, x₃ and i, j, k, l, m, n, and o as independent imaginary numbers as the basis coordinate representing seven different time dimensions, c_i is the speed of light of the respective temporal dimensions t_i .

It is identical to Octonion :  

q = x + ic₁t₁ + jc₂t₂ + kc₃t₃ +lc₄t₄ + mc₅t₅ + nc₆t₆ + oc₇t₇ 

where x = x(x₁ , x₂ , x₃)

The physical laws prevailing in such a system would be extremely complicated. Under the internal symmetry, we can make it much simpler by changing the extra time dimensions into spatial ones transforming the system to get a system consisting of 9-space embedded in 10-dimensional ambient spacetime.

Its mathematical formulation then becomes a simple ordinary complex number:

q = x₁ +x₂ + x₃ + x₄ +x₅ + x₆ + x₇ + x₈ + x₉+ oc₇t₇

Denoting x = x (x₁, … x₉), we get a simple form:

q = x + oc₇t₇

e)   For example, if we have a system consisting of 6-brane embedded in 10-ambient spacetime (a system with 6 space dimensions and 4 time dimensions): 

q = x₁ +x₂ + x₃ + x₄ +x₅ + x₆ +lc₄t₄ + mc₅t₅ + nc₆t₆ + oc₇t₇ 

Usually we consider such a system having only one time dimension and disregard the other three: 

q = x₁ +x₂ + x₃ + x₄ +x₅ + x₆ +lc₄t₄ 

the solution of this formulation would be the only approximation of the former.

f)   The dimensions of macro-cosmos are assumed to be [quasi] infinite. It happened that we need only an ambient spacetime having 11 dimensions embedding a 10-brane  as in the case of supergravity theory.

g)   In such a diagram, simultaneous events would flatten their loci, an n-surface (hyperinterface, brane) embedded in (n+1) ambient spacetime; otherwise, the surface would not be flat. Figure-1B shows events which happen simultaneously at a certain time dimension t₂ while they do not happen simultaneously at a lower time dimension t₁ (Figure-1A).

Multiple Time Dimensions, why not?

Is Quantum World beyond the Physical Reality?

The quantum reality is so weird as compared to the ordinary classical pictures that hardly anybody talks openly about its very existence. For most physicists the mathematical formalism of such quantum mechanics that talks.

Most physicists, who look at the quantum particles' behavior, think that they are dealing with rigid body mechanics.  They are all wrong. The quantum mechanics is closer to fluid mechanics rather than the rigid body mechanics. Just as in fluid mechanics, we are dealing with a continuum rather than a single particle, and therefore, there is no need to keep track of individual particles.

In quantum mechanics, one should not pose a question like: "What is the position in the space of a [quantum] particle as a function of time?" Rather,  it is more appropriate to ask: “At some point in space what is the velocity, acceleration, and thermodynamic properties at that point in space as a function of time?” The mathematical model used to describe such mechanics is called Eulerian as opposed to Lagrangian which is used to keep track of an individual particle as in rigid body dynamics¹.   

It should be noted, however, that in quantum mechanics we are not dealing with a movement in bulk but on the surface of the fluid (Figure-1A). We recall that the real world we live in could be modeled as a 3-hypersurface or more precisely a hyper-interface located in between two oceans of the opposing energies (Figure-1B).

At such surface, all of the quantum particles movements are up and down just like the movement of particles in the individual water wave propagating along the surface of a still pond. The up and down motions are the projection of the quantum circular movements whose circumference equal to quantum action, Planck number (h), and whose radius is equal to Dirac's Planck number.  

So, there is no such a quantum particle flies forward as a bullet does. What physicists perceive as a single quantum particle enduring in time [regardless whether it is moving or in rest] is, in fact, different ephemeral particles successively appearing and disappearing as time passes by.

To give a clear picture of this phenomenon, let us cite a child story about the imbalanced race between the deer and snails.  Here is the excerpt: in the middle of the jungle there lived a smart deer that had defeated all but some of the inhabitants.  It happened that in the darkness of twilight the deer was unintentionally about to step on a snail unseen behind the grasses. The angry little creature challenged him to race by the following day, which the deer confidently accepted.

During the night, the petite snail coordinated hundreds of his friends to stand in line under-covered behind the grasses along the racing path. As the race progressed, the deer  was wondering about the position of his rival and shouted: “Hello dear friend, where are you?” The snail which stood just in front of him responded: “I am here.” The deer was bewildered and so repeatedly monitored from time to time up to the final point. After that, he was always agitated as nobody told him about the secret of the presence of so many snails that he had thought as a single one.

Another but much more old metaphor on the quantum reality teaches us about the universe which resembles a gigantic flame of a candle. Like the flame, the world is always changing and never be the same at any instant of time. The whole world and all its contents are perpetually created and annihilated. As in Galilean dynamics,  we may interpret that the physical space evaporates completely as one moment passes, and reappears as a completely different space as the next moment arrives². 

Figure-2 shows the schematic description of the physical space represented as a 3-front wave propagates across the 4-surface (spacetime). The wave (3-space) disappears completely as one moment passes, and reappears as a completely different wave as the next a moment arrives; and so the front wave is propagating forwards with time. 

Finally, we come to a more detail subject which combines the phenomena of hydrodynamics with electromagnetism. As the wave is propagating between two oceans of the positive and negative energies, we deal with some sorts of magnetohydrodynamics which takes into account the interaction of electrically conducting fluids and electromagnetic fields (Figure-3).

The perpetual creation and annihilation of quantum particle and its anti-particle, as well as the classical fields, is the result of some sorts of interactions of quantum fields and the hyper-interface (brane). The interplay  between that two opposite "electrically"  conducting fluids generates the quantum fields. 

The result is that we get a sort of cosmic motion picture where the images are projected on a gigantic screen (3-brane) in which the images perpetually appear and disappear altogether with the screen at the rate of 10⁴⁴ images per second. The projected images stand for the whole content of the universe: planets, stars, galaxies, super-galaxies, a cluster of galaxies and so forth. 

References:

1.   Hughes, W. F., and Brighton, J. A.: "Fluid Dynamics," Schaum's Outline Series, New York, 1967, p. 2.

2.     Penrose, R.: "The Road to Reality," Vintage Books, London, 2004, p. 387.

Is Quantum World beyond the Physical Reality?

The Brane Theory as It should be

The brane theory is the derivative of the string theory, a mathematical model which was built to simulate the empirical particle interactions. The theory holds on the premise that the most basic indivisible objects underlying all matter are tiny vibrating segments or loops of the one-dimensional string-like entity.

In its later development, string theorists discovered that the strings do not freely move throughout the whole spacetime continuum but are constrained along the surface of membrane-like objects, coined as "branes," whose dimensions may extend over some, but not all of their embedding space's dimensions.

The branes are not just loci of matters and forces interactions, but also real objects which can be slack, wiggling and moving, or stretched tight. Branes are distinguished not only by the number of their dimensions in which they extend but also by their charges, their shape and tension¹.

Despite the development intensity of the theory, the brane theorists are not yet to know whether their branes exist in the real world. They are like a blind man wondering about the big picture of the elephant after having felt the ear and the trunk of such animal.

1.   The spontaneously symmetry breaking of the spacetime

The brane theory proves that the spacetime world model as currently conceptualized is wrong. It is the existence of a 3-brane embedded in such spacetime that makes the latter's dimensions differentiated. Otherwise, the spacetime's dimensions are equal, in the sense that the spacetime is perfectly symmetric, homogeneous and isotropic ^a).

Paradoxically, as Lisa Randall remarked, many physicists think otherwise²:" They did not want to include branes in a physical realization of string theory because brane violated their intuition that all dimensions are created equal. Brane distinguishes certain dimensions – those along the brane are different from those that extend off it – whereas the known laws of physics treat all directions the same. Why should string theory be different?”

In fact, following the Minkowski’s discovery [1908] on the inextricability of the space and time, physicists have confusedly taken for granted the inequality of the dimensions of the spacetime, the union of the space and time³. They thought that the light cone system set up in every point within such spacetime could establish order and preserve the causality.

The special relativity, as currently conceptualized, is inconclusive. In order to explain the inequality of such continuum's dimensions, the physicists should include in their world creation scenario the spacetime's spontaneous broken symmetry. As it happens, the 3-brane comes into being in between the two spacetime's distinct halves, in which the dimensions along the brane become spatial and those off it temporal dimensions.

It is just like the separation of oil and water which we can observe in our daily [3-dimensional ambient] life ^b). The dimensions along the interface, because of the effect of the interfacial tension, would be different from those off it.

The gravity constant (G) that we are familiar with is nothing but the interfacial tension of the 3-brane embedded in 4-spacetime. Consequently, the gravity field like the other classical fields is trapped along the brane, not propagate off it as what the brane theory currently assumes ^c). The fields that may propagate off the brane are quantum fields including those of Higgs.

2.   Why a brane traps matter and classical fields?

Randall took for the analogy of trapping matter on a brane among other things water droplets on a shower curtain which travel only along the curtain's surface.

We wish here to provide a better and physically more appropriate analogy for describing the braneworld model. Matters are analogous to tiny flashes appearing and disappearing on the surface of a giant TV-screen.  The impact of streams of electrons fired onto and hit the screen resulting in the generation of these tiny flashes.

The seemingly trapped matters on the brane are tiny sparks appear and disappear on the TV screen-like brane. These tiny sparks, which are quantum in size^d), are generated as the effect of the quantum fields (Higgs fields) hitting in the normal direction through the brane.

The quantum fields are themselves generated as the result of the constant interplay between the positive and negative energies located at the opposite sides of the brane (Figure-1A). As the quantum fields piercing through the brane, the classical fields including those of light are generated, under the right-hand rule, propagating along the surface of the brane (Figure-1B). 

3.   Why there exist various dimensional branes?

So far we have shown that the special relativity theory ultimately leads us to the union of the spacetime and energy.  The spacetime has faded away into a mere shadow to become just the geometry of the energy, the only independent reality in nature.

Some physical theories identify the existence of higher dimensional manifolds (spacetimes). It leads us to the conclusion that energies of higher dimensions corresponding to such spacetimes should exist as well.

The energy in itself inherently consists of a pair of positive and negative components. As the opposing energy components tend to segregate, all of those spacetimes are highly unstable. The segregation of the positive and negative energies causes the spacetime to split in two, creating a brane in between.

The splits of those spacetimes are taking place starting from the highest dimensional spacetime down to the lowest one, which is nothing but our universe, the 3-brane (Figures-2 and 3).

We may imagine an interface of oil and water as a 2-dimensional slice of a 3-dimensional liquid, similarly, a 3-brane as 3-slice of 4-dimensional spacetime, 4-brane as a 4- slice of 5-spacetime and so on. We should underline that the dimensions along the brane are always spatial and off the brane temporal, and never mix them up ^e).

4.   Why the branes exist in a pair?

The brane theory includes the existence of two parallel branes bind higher-dimensional worlds such as Horava-Witten and Randall-Sundrum brane-worlds. In such world models, the standard model particles are constrained on one brane, and non-standard particles are sequestered on the other branes.

Why does such a pair of parallel branes exist?

A brane, like a piece of paper, has a very thin thickness and two opposite sides. The two parallel branes that the physicists refer to are not independent of each other but just two different sides of a single brane.

As one side of the brane faces positive energy, and the other side faces the negative energy, the two brane's sides have accordingly opposite charges (Figure-4). For example, under a 4-ambient space, the positive side of the 3-brane contains matters while the negative side sequesters antimatters. 

This kind of brane world-model can be extended merely to the higher dimensional world. Within the 4-spacetime framework, the distance between these two sides of brane might be equal to Planck distance of 10^-33 cm (10^-44 second), and it would be much more significant in a higher dimensional spacetime. 

5.   Why 10- or higher-dimensional branes exist in nature?

The brane theory consists of two theories of10- and 11-manifold. To explain why such duality may arise, we have to refer to the mathematical concept of hypersurface whose geometry is equivalent to that of the brane. We define a hypersurface as a multi-dimensional surface having one or more dimensions lower than those of the embedding space.

A rule dictates that an n-dimensional curved hypersurface does have a solution if and only if it is embedded in an ambient space having at least ½ n(n+1)-dimensions⁴. Accordingly, a 4-brane (spacetime) requires an ambient space containing at least ten dimensions.  It seems that the 11-ambient space provides enough room for such a world model has a solution than the 10-ambient space does.

Notes:

a.  In the ancient cosmology, the condition where the spacetime's dimensions are still equivalent, in the sense that the time is not yet divided (there is no present, past and future), is termed as chaos and the spacetime 'eon.'

b.   Surprisingly, this kind of analogy had been proposed a long time ago, since the dawn of the history, by Enmeduranki, the king of Sippar, Babylon, who lived and reigned before the Flood⁵

c.  As the graviton is a close-loop string having no ends, the whole parts of its length are pinned down on the brane, on the contrary of what happened in the brane theory.

d.  We guess it is more appropriate to use the term of quark as the acronym of quantum spark, the underlying nature of the fundamental particles, not limited to those which compose the nucleons.

e.  It may lead to the establishment of multidimensional times theory which is naturally more appropriate than one-dimensional time.

References:

1.   Randall, L.: "Warped Passages," Harper, New York, 2006, p. 305-306.

2.   Idem, p. 307

3. Einstein, Albert: The Meaning of Relativity, Princeton University Press, New Jersey, Fifth Edition, 1954, p. 31

4.  Sokolnikoff, L.S: "Tensor Analysis," Wiley Toppan, Second Edition, New York, 1964, p.205

5. Wright, J.E.: The Early History of Heaven, Oxford University Press, Oxford, 2000, p. 43.

The Brane Theory as It should be