We used to conceptualize the geometry elements such as point, line,
surface and space as having, respectively, zeroed, one, two and three
dimensions. There is nothing wrong with that as far as we are dealing with
abstract objects such as a corner point between a floor and two walls, meeting
line between ceiling and wall, table's surface or hall's spaciousness.
However, we cannot apply such a concept for real
bodies, whatever the size is. A grain of sand is not a zeroed-dimensional
object, but a three-dimensional cubic-like body has small length, width, and
thickness. A string is a three-dimensional long cylindrical object having a
small section. Similarly, a piece of paper is a three-dimensional surface
object whose thickness is very thin (Figure-1). Had their thickness been
reduced to zero, those objects would all have gone into thin air.
Nature does not seem to give any exception to more fundamental entities
such as space or any other higher-dimensional spacetimes. For their existence
to have physical meaning, all those bodies should have thickness. It implies
that space or spacetime, whatever its dimensions, should embed in an ambient
spacetime of at least one dimension higher. So be the next body, it embeds in
turn in another much higher manifold (Figure-2). This kind of infinite regress makes us
believe that nature is vast and infinite, not only its wide expanses but also
its dimensions.
System and Surroundings
Now, the formulation of the laws of nature depends naturally on which
system we choose. Suppose we want to formulate physical laws within a system of
an m-dimensional spacetime embedded in
N-dimensional ambient manifold, we get, then, physical laws of a system
having (N-m) extra dimensions. The directions of these dimensions determine
those of the spacetime's thicknesses pointing outwards away from it.
We can describe the same physical laws in a much
simpler system where the same N-ambient space embedding (N-1)-hypersurface,
instead of an m-spacetime. The thickness of such a hypersurface has the same
direction as that of the Nth dimension pointing outward away from
it.
The laws of nature in the former system have very complex formulations
and are difficult to resolve, as the system has too many extra-dimensions and,
hence, fewer symmetries. The laws of
nature in such a system are relatively more straightforward as the system has
only one extra-dimension and is highly symmetric.
We canThe laws of nature can be best described when the number of the
dimensions of the ambient space embedding the system is large enough which
"stretches" out the hypersurface to become completely flat and
perfectly symmetric.
How do we determine the dimensions of the ambient
space (N) vis-a-vis that of the embedded spacetime (m)? There is a minimum
requirement for the number of the ambient space's dimensions for the spacetime
can be "properly" embedded in the ambient space. The [non-flat]
m-spacetime can be embedded in N-manifold only if at least N = ½ m(m+1) 1). The metric
tensor of the m-spacetime dictates that the ambient space should have that
amount of dimensions for all of its components can be properly defined.
Based on the above rule, the 2-surface requires 3-ambient space for which we do not doubt it.
The non-flat 3-space, in our surprise,
requires 6-ambient spacetime, not to mention the 4-spacetime which
requires 10-ambient manifold. It may indirectly explain why we have three
generations of elementary particles and the 10-ambient manifold as revealed in
the current theoretical physics.
Multidimensional Time
Now, what these dimensions are we talking about? As we have discussed
previously, the spacetime is the physical manifestation of energy. In its
original state, the spacetime was utterly symmetric. All of its dimensions are
indistinguishable, and they are all "temporal." When the respective
energy segregates into the positive and negative energies, the [temporal]
spacetime's dimensions along the interface [separating those opposing energies]
are transformed into spatial dimensions.
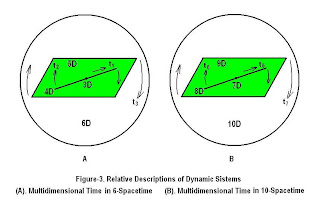
For the classical 4-spacetime, the energy
segregation transforms three of the spacetime's temporal dimensions along the
interface into spatial (Figure-3). In a 6-spacetime, the energy's segregation
transforms the spacetime's five temporal dimensions along the interface into
spatial dimensions. The same case also prevails for the 10-spacetime., where
nine temporal dimensions along the interface become spatial.
The temporal dimensions t1, t3
and t7 related to the 4-, 6- and 10-spacetimes, respectively, are different
from each other. It is against the mainstream premise which tacitly asserts
that there is only a time dimension in nature.
Based on the rule we have, a 4-spacetime requires a 10-ambient space for
the physical laws to have solutions. However, as we have in this case 3 spatial
dimensions and 7 [imaginary] extra-temporal dimensions, the physical laws we
get would be very complicated. It is imperative, therefore, to have the same
laws applied to a system consisting of a 10-ambient space embedding
9-hypersurface, which are simpler as we have only one imaginary temporal
dimension on top of the nine real ones.
It is more or less what physicists have done in developing the string
theory, except that the extra-dimensions were assumed being curled into tiny
loops. Besides, the temporal dimension of the system was assumed to be the same
as that of ordinary time. Such wrong assumptions have been put forward because
mainstream physics holds the premise that time is one-dimensional as previously
mentioned.
The relativity theory should rigorously hold the equivalence of space
and time dimensions. The spatial and temporal dimensions should be transferable
to each other depending on the system they become part. The extra dimensions
are indetectable not because they curl into tiny loops but because they are temporal.
Supermanifold and Supersymmetry Generators
Physicists have many problems with their mathematical propositions as
they used to conceptualize the spacetime as a standalone basis. Under such a
concept they have taken the more significant part of the reality out of the
system. Such as is the case of the Big Bang theory, which is entirely Platonic,
a system without any geometrical thicknesses, surrounding, nor even 3-space.
A reader of the Scientific American2) once
asked: "Where is the universe expanding to?" The authoritative answer from the expert was:
"... the universe's expansion does not push it into new territory - rather
the spacetime grid itself is expanding".
The issue has arisen again and again since the Big Bang theory was put
forward, as only a few people were satisfied with such an explanation. The
excellent answer should be that the universe is expanding to at least the
10-dimensional ambient space, and not into nothing.
To make their model closer to the reality, some
physicists artificially introduced what they called supersymmetry generators,
replacing the thicknesses which they have "forgotten" to incorporate
in their mathematical model. They call this manifold having thicknesses
"Supermanifold"3).
The physicists should put forward the problems of embedding at the forefront of physical researches and develop a more holistic model instead of a piecemeal one.
The physicists should put forward the problems of embedding at the forefront of physical researches and develop a more holistic model instead of a piecemeal one.
References:
1. Sokolnikoff,
L.S.: "Tensor Analysis," Wiley Toppan, Second Edition, New York,
1964, p. 205
2. Kashlinsky,
A.: "Where is the Universe Expanding to?", Scientific American, (Ask
the Experts Forum), May 2007, p. 104
3.
Penrose R.:
"The Road to Reality," Vintage Books, London, 2005, p. 879.


No comments:
Post a Comment