Space Thickness, Supermanifold and Multidimensional Time

We used to conceptualize the geometry elements such as point, line, surface and space as having, respectively, zeroed, one, two and three dimensions. There is nothing wrong with that as far as we are dealing with abstract objects such as a corner point between a floor and two walls, meeting line between ceiling and wall, table's surface or hall's spaciousness.

However, we cannot apply such a concept for real bodies, whatever the size is. A grain of sand is not a zeroed-dimensional object, but a three-dimensional cubic-like body has small length, width, and thickness. A string is a three-dimensional long cylindrical object having a small section. Similarly, a piece of paper is a three-dimensional surface object whose thickness is very thin (Figure-1). Had their thickness been reduced to zero, those objects would all have gone into thin air.

Nature does not seem to give any exception to more fundamental entities such as space or any other higher-dimensional spacetimes. For their existence to have physical meaning, all those bodies should have thickness. It implies that space or spacetime, whatever its dimensions, should embed in an ambient spacetime of at least one dimension higher. So be the next body, it embeds in turn in another much higher manifold (Figure-2).  This kind of infinite regress makes us believe that nature is vast and infinite, not only its wide expanses but also its dimensions.

System and Surroundings

Now, the formulation of the laws of nature depends naturally on which system we choose. Suppose we want to formulate physical laws within a system of an m-dimensional spacetime embedded in  N-dimensional ambient manifold, we get, then, physical laws of a system having (N-m) extra dimensions. The directions of these dimensions determine those of the spacetime's thicknesses pointing outwards away from it.

We can describe the same physical laws in a much simpler system where the same N-ambient space embedding (N-1)-hypersurface, instead of an m-spacetime. The thickness of such a hypersurface has the same direction as that of the N^th dimension pointing outward away from it.

The laws of nature in the former system have very complex formulations and are difficult to resolve, as the system has too many extra-dimensions and, hence, fewer symmetries.  The laws of nature in such a system are relatively more straightforward as the system has only one extra-dimension and is highly symmetric.

We canThe laws of nature can be best described when the number of the dimensions of the ambient space embedding the system is large enough which "stretches" out the hypersurface to become completely flat and perfectly symmetric.

How do we determine the dimensions of the ambient space (N) vis-a-vis that of the embedded spacetime (m)? There is a minimum requirement for the number of the ambient space's dimensions for the spacetime can be "properly" embedded in the ambient space. The [non-flat] m-spacetime can be embedded in N-manifold only if at least N = ½ m(m+1) ¹⁾. The metric tensor of the m-spacetime dictates that the ambient space should have that amount of dimensions for all of its components can be properly defined.

Based on the above rule, the 2-surface requires  3-ambient space for which we do not doubt it. The non-flat 3-space, in our surprise,  requires 6-ambient spacetime, not to mention the 4-spacetime which requires 10-ambient manifold. It may indirectly explain why we have three generations of elementary particles and the 10-ambient manifold as revealed in the current theoretical physics.

Multidimensional Time

Now, what these dimensions are we talking about? As we have discussed previously, the spacetime is the physical manifestation of energy. In its original state, the spacetime was utterly symmetric. All of its dimensions are indistinguishable, and they are all "temporal." When the respective energy segregates into the positive and negative energies, the [temporal] spacetime's dimensions along the interface [separating those opposing energies] are transformed into spatial dimensions.

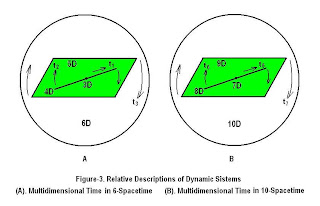
For the classical 4-spacetime, the energy segregation transforms three of the spacetime's temporal dimensions along the interface into spatial (Figure-3). In a 6-spacetime, the energy's segregation transforms the spacetime's five temporal dimensions along the interface into spatial dimensions. The same case also prevails for the 10-spacetime., where nine temporal dimensions along the interface become spatial.

The temporal dimensions  t1, t3 and t7 related to the 4-, 6- and 10-spacetimes, respectively, are different from each other. It is against the mainstream premise which tacitly asserts that there is only a time dimension in nature.

Based on the rule we have, a 4-spacetime requires a 10-ambient space for the physical laws to have solutions. However, as we have in this case 3 spatial dimensions and 7 [imaginary] extra-temporal dimensions, the physical laws we get would be very complicated. It is imperative, therefore, to have the same laws applied to a system consisting of a 10-ambient space embedding 9-hypersurface, which are simpler as we have only one imaginary temporal dimension on top of the nine real ones.

It is more or less what physicists have done in developing the string theory, except that the extra-dimensions were assumed being curled into tiny loops. Besides, the temporal dimension of the system was assumed to be the same as that of ordinary time. Such wrong assumptions have been put forward because mainstream physics holds the premise that time is one-dimensional as previously mentioned.

The relativity theory should rigorously hold the equivalence of space and time dimensions. The spatial and temporal dimensions should be transferable to each other depending on the system they become part. The extra dimensions are indetectable not because they curl into tiny loops but because they are temporal.

Supermanifold and Supersymmetry Generators

Physicists have many problems with their mathematical propositions as they used to conceptualize the spacetime as a standalone basis. Under such a concept they have taken the more significant part of the reality out of the system. Such as is the case of the Big Bang theory, which is entirely Platonic, a system without any geometrical thicknesses, surrounding, nor even 3-space.

A reader of the Scientific American²⁾ once asked: "Where is the universe expanding to?"  The authoritative answer from the expert was: "... the universe's expansion does not push it into new territory - rather the spacetime grid itself is expanding".  The issue has arisen again and again since the Big Bang theory was put forward, as only a few people were satisfied with such an explanation. The excellent answer should be that the universe is expanding to at least the 10-dimensional ambient space, and not into nothing.

To make their model closer to the reality, some physicists artificially introduced what they called supersymmetry generators, replacing the thicknesses which they have "forgotten" to incorporate in their mathematical model. They call this manifold having thicknesses "Supermanifold"³⁾. 

The physicists should put forward the problems of embedding at the forefront of physical researches and develop a more holistic model instead of a piecemeal one.

References:

1.   Sokolnikoff, L.S.: "Tensor Analysis," Wiley Toppan, Second Edition, New York, 1964, p. 205

2.  Kashlinsky, A.: "Where is the Universe Expanding to?", Scientific American, (Ask the Experts Forum), May 2007, p. 104

3.    Penrose R.: "The Road to Reality," Vintage Books, London, 2005, p. 879.

Space Thickness, Supermanifold and Multidimensional Time

Hypersurface, the Extrinsic View of the World

Any application of the law to a discrete portion of the universe or even something else more prominent such as the possible multiverses requires the description of a system and its surroundings. A system can be any region of space, the whole universe itself or any region of multiverses selected for study and set apart [mentally] from everything else, which then becomes the surroundings.

There are two ways on how we can geometrically describe the world, i.e. intrinsically or extrinsically. Let us take an example on how we describe a lower dimensional object such as a surface. We can describe the properties of surfaces without reference to the space in which the surface is embedded as intrinsic properties. We can imagine that in this particular case the properties of the surface are analyzed from two dimensional flat being living in such surface, whose universe is determined solely by [two] surface parameters. In this intrinsic geometry a pair of isometric surfaces, a cone and cylinder, for example, are indistinguishable.

These surfaces appear to be quite distinct to an observer examining them [extrinsically] from a reference frame located in the space in which the surfaces are embedded. Geometrically, an entity that provides a characterization of the shape of the surface as it appears from the enveloping space is the normal line to the surface^[1].


Now let us turn to examine the concepts from the geometry of higher dimensional metric manifolds which are of our primary interest. Many of the concepts are straightforward generalizations of ideas introduced in the study of surfaces embedded in the three-dimensional [Euclidean] manifolds. For the visualization purposes, we wish to put forward the relative depictions of the n-dimensional world viewed intrinsically as standing alone n-hyperspace and viewed extrinsically as an n-hypersurface embedded in (n+1) or higher dimensional hyperspace (Figure-1).

An n-dimensional flat hypersurface can be entirely embedded in an (n+1) dimensional hyperspace, but as the hypersurface is curved, it needs much spacious ambient. Now, under what circumstances an m-dimensional variety (hypersurface) can be embedded in the n-dimensional Euclidean manifold (hyperspace)? The answer is that the m-hypersurface can be wholly embedded in hyperspace without restraint on whatever direction it might curve if and only if such a hyperspace has at least n = ½ m (m+1) dimensions. We call the latter as an allowable embedding hyperspace to a particular hypersurface.

It means that there are a total of [1/2m (m+1)-m] normal lines to the "surface" of such a hypersurface. In a dynamic condition where the hypersurface moves relative to the ambient hyperspace this-extra dimensions are identified as extra [temporal] dimensions, not the ones which curled in tiny looped as the string theory hypothesizes.

Einstein had developed the relativity theory both special and general relativity theories based on intrinsic geometry. It is the weakness of the relativity theory which ignores the surroundings representing more than 99% of the whole reality we are longing to recognize. No wonder the Big Bang theory, the derivation of the relativity theory, can only take into account 5% out of the total matter and energy affecting the known universe.


Intrinsically, we consider the independent variables of the metric tensor of Einstein four-dimensional spacetime as just mathematical variables having no physical significance. However, when we see the world extrinsically, those variables of the metric tensor are nothing but the manifestation of the underlying coordinates – the dimensions of the embedding hyperspace.

We can achieve the unification theory if we describe the world as a curves hypersurface at least in term of parameters of its minimum allowable embedding hyperspace.

The concept of brane, the representation of the world as a hypersurface is already in the right track except for the concept of its ambient hyperspace. The brane is not like a piece of paper floating around in thin air, but more like an interface of higher dimensional watery like substances – higher dimensional of positive and negative pure energies (Figure-2).

Hypersurface, the Extrinsic View of the World